Latest News
 A Milestone Moment: The College of Education and Professional Studies Celebrates its 25,000th Degree
A Milestone Moment: The College of Education and Professional Studies Celebrates its 25,000th Degree
Tuesday - December 16, 2025
The University of South Alabama College of Education and Professional Studies reached a historic milestone during Fall Commencement on Friday, Dec. 12, awarding its 25,000th degree.
Read more
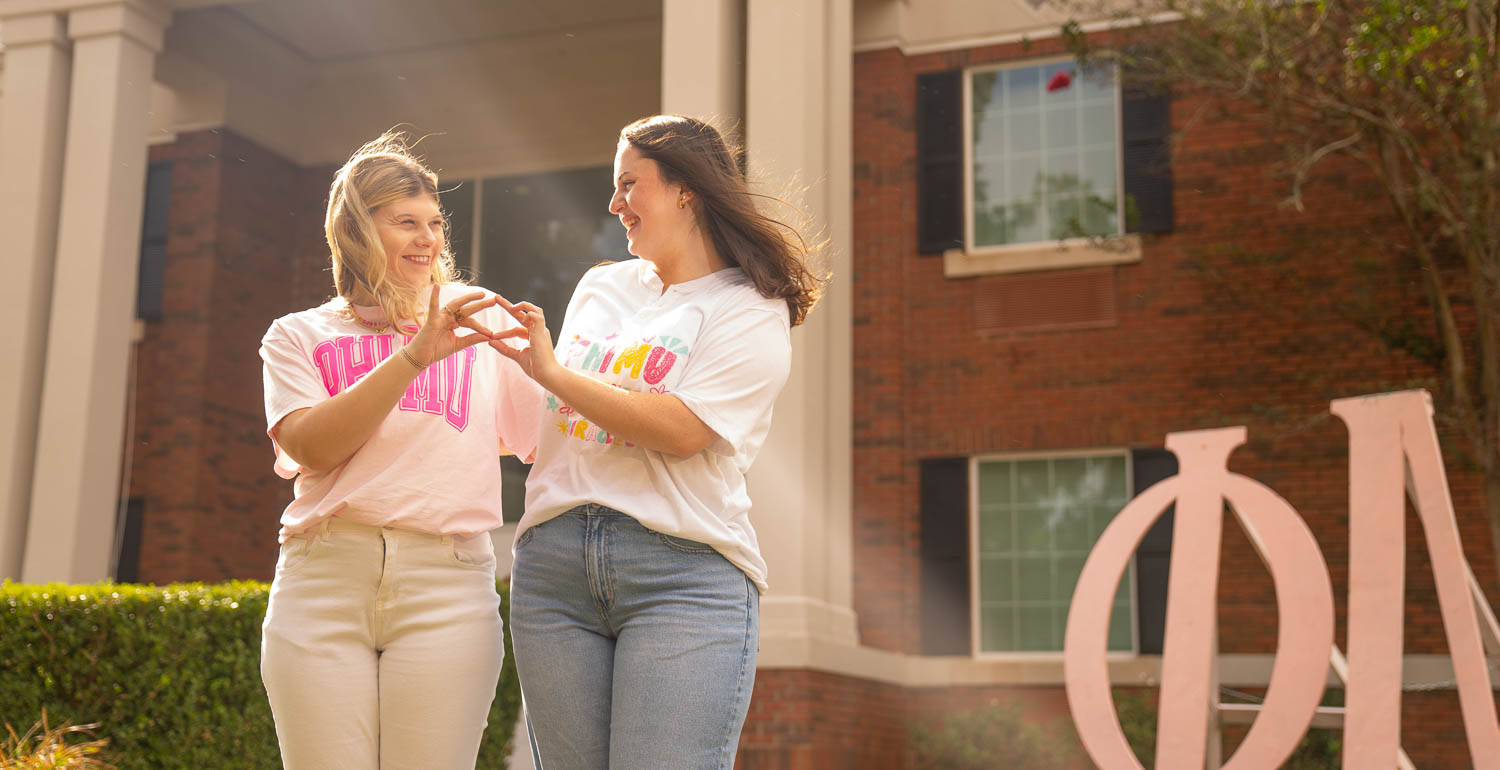 Building Sisterhood, Breaking Barriers
Building Sisterhood, Breaking Barriers
Tuesday - November 4, 2025
Marion McLaughlin becomes the first PASSAGE USA student to pledge a Greek organization during a record year. Her 'big' is also a peer mentor in the program designed to help those with with intellectual disabilities navigate the job world.
Read more
 Institutional Effectiveness Welcomes Third Cohort of LevelUP Fellows
Institutional Effectiveness Welcomes Third Cohort of LevelUP Fellows
Thursday - October 30, 2025
The Office of Institutional Effectiveness has announced the third cohort of LevelUP Fellows for the 2025-2026 academic year.
Read more