Geography
"What do GEOGRAPHERS do?"
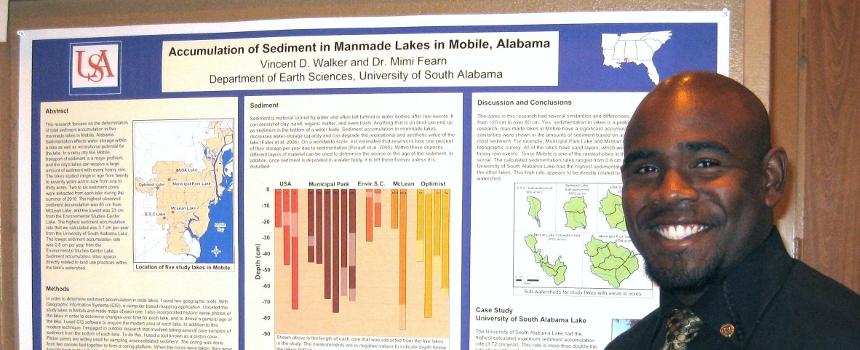
Most people in the United States are exposed to geographic education only at the elementary school level. As a result, there is a widespread misconception that Geography is limited to boring memorization of locations of countries, states, capital cities, major physical landmarks and export products. The truth is that modern geography is an exciting science producing research of great value to government interests, planning agencies, and private businesses.
What Do Geographers Do?
 The term geographer is rarely used either in the title or description of career positions,
but geography majors possess unique analytical skills that enable them to succeed
in a remarkable range of occupations. Employers welcome the geographer’s comprehensive
knowledge of natural and social sciences coupled with his/her distinctive understanding
of spatial patterns. There is a high demand in business, industry, and government
for geographers with training in physical geography, human geography, and geographic
information science (GIS).
The term geographer is rarely used either in the title or description of career positions,
but geography majors possess unique analytical skills that enable them to succeed
in a remarkable range of occupations. Employers welcome the geographer’s comprehensive
knowledge of natural and social sciences coupled with his/her distinctive understanding
of spatial patterns. There is a high demand in business, industry, and government
for geographers with training in physical geography, human geography, and geographic
information science (GIS).
Physical geographers study weather, climate, water and coastal processes, plant and animal distributions, landforms, soils, and natural hazards. Their objective is to improve the understanding of the way the environment operates, both naturally and in response to human-induced changes. Physical geographers evaluate the potential of natural resources, make environmental impact assessments, monitor environmental change, map exotic species expansion, and determine the risks of harm from natural hazards such as storms, volcanic eruptions, landslides, and floods.
Human geographers examine economic, social and political dimensions of the landscape. They study population, agriculture, industry, tourism, cities, transportation networks, migrations, commodity flows, political units, and behavioral patterns. Their objective is to improve our understanding of how people use the land and help plan more rational uses of natural resources that will benefit society while protecting the environment from excessive deterioration.
Both physical and human geographers direct their attention toward two fundamental research questions:
“Where are things located?”
“Why are they located there?”
Careers in Geography
 A Geographer may work in the private or public sector as a:
A Geographer may work in the private or public sector as a:
- demographer
- transportation analyst
- cartographer
- geographic information systems analyst
- market researcher
- travel consultant
- real estate developer
- resource analyst
- environmental consultant
- surveyor
- remote sensing specialist
- high school teacher
- location research analyst
- city/regional planner
- traffic planner
- park ranger
- soil conservationist
- soil surveyor
- administrative analyst
- waste management coordinator
- university professor
- cultural affairs manager
Ready to take the first step? Want more information on what Geography at the University of South Alabama has to offer? Contact us, and we will be happy to help you begin your journey to a fun and rewarding career as a Geographer!